18 جولای 2020
مقایسه احتمال ارتکاب جرم در مجردها و متاهل ها
یکی از انواع تبعیض رایج در فرهنگ ما، تبعیض علیه مجرّدها است؛ به ویژه مردان مجرّد. از ممنوعیت در تردد به محلهای خاص گرفته تا آگهی استخدام؛ همه جا میتوانید آن را ببینید. مستقل از هر چیزی، این کار یک اشکال آماری و ریاضی هم دارد. میخواهم در این رشته، به این موضوع بپردازم.
ابزاری که اینجا استفاده میکنم، قانون بیز (Bayes’ Rule) است، که یکی از کاربردیترین روابط ریاضی است و بخش زیادی از روشهای هوش مصنوعی، اساسا متکی به آن هستند.
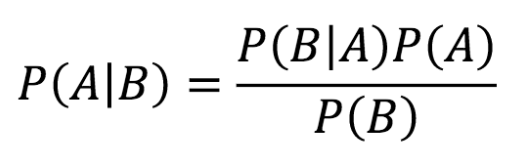
این نمادها و تعاریف را در نظر بگیرید:
- مجرد بودن: S
- متأهل بودن: M
- مجرم بودن: C
- مجرم نبودن: N
منظور از مجرم بودن نیز، ارتکاب به یک جُرم خاص و کاملا فرضی است. حالا (P(S یعنی احتمال مجرد بودن و (P(C یعنی احتمال ارتکاب به آن جرم مفروض.
این که محدودیتی برای مجردها در نظر گرفته میشود یا تبعیضی علیهشان روا داشته میشود، احتمالا به این دلیل است که احتمال مجرد بودن یک فرد مجرم، بیشتر از متأهل بودن او است. اما من میخواهم نشان بدهم که الزاما این طور نیست. یعنی مبنای فکری این تبعیضها، یک خطای آماری و منطقی است.
فرض کنید ۳۵ درصد افرادی که به سن ازدواج رسیدهاند، هنوز مجرد هستند؛ ۶۵ درصد باقی مانده هم، ازدواج کرده و متأهل هستند. ضمنا، فرض کنید طبق آمار، ۵ درصد از مجردها یک جرم خاص را مرتکب میشوند؛ اما همین کسر در میان متأهلین، ۳ درصد است. یعنی احتمال ارتکاب جرم میان متأهلها، کمتر است.
این موارد، اگر به زبان ریاضی نوشته شوند، به این صورت خواهند بود:
- P(S) = ۰/۳۵
- P(M) = ۰/۶۵
- P(C|S) = ۰/۰۵
- P(C|M) = ۰/۰۳
میتوان درصد ارتکاب جرم در کل جامعه را به این صورت حساب کرد:
- P(C) = P(C|S)×P(S) + P(C|M)×P(M) = ۰/۰۳۷
تا اینجا به نظر میرسد که متأهلین قابل اعتمادتر هستند. اما هنوز برای نتیجهگیری زود است. ما باید احتمال شرطی (P(S|C و (P(M|C را حساب کنیم. یعنی، احتمال این که یک فرد مجرم، مجرد است یا متأهل. راه محاسبه این احتمال، استفاده از قانون بیز است. احتمال مجرد/متأهل بودن یک مجرم، با استفاده از قانون بیز به این صورت محاسبه میشود:
- P(S|C) = P(C|S)×P(S)÷P(C) ≃ ۰/۴۷۳
- P(M|C) = P(C|M)×P(M)÷P(C) ≃ ۰/۵۲۷
علی رغم این که توزیع اولیه حاکی از کمتر بودن آمار جرم در میان متأهلین بود، اما احتمال متأهل بودن یک مجرم، ۵/۴ درصد بیشتر از مجرد بودن اوست. دلیل محاسبه (P(S|C و (P(M|C آن است که احتمال پیشین میگوید که احتمال خلافکار بودن یک مجرد بیشتر است. اما فرض کنید یک خلافکار فرضی را گرفتهاند. احتمال این که وی متأهل باشد، بیشتر است. چون مساحت احتمالی بیشتری را پوشش میدهند؛ بر خلاف آنچه از توزیع احتمال پیشین برداشت میشود.
آنچه در این تبعیضها اتفاق میافتد، کاهش تعداد یا کسر نسبی (و به عبارتی احتمال) مجرم بودن است. یعنی معیار نسبی، که کاملا هم غلط نیست، معیار تصمیمگیری و انتخاب است. یک زاویه نگاه متفاوت هم این است که ببینیم تعداد یا کسر مطلق هر گروه در مجرم بودن چقدر است؟
یعنی بررسی کنیم و ببینم این گروهی که آمار جرم و جنایت در میانشان پایین است، چه کسری از همه جرمهای جامعه را مرتکب شدهاند و چه باری را به جامعه تحمیل کردهاند؟ هدف نهایی این است که نشان داده شود، فرضا شرط تأهل، شرط کافی یا لازم برای تعهد نیست.
در واقع، فرض کنید که از مردم در خصوص وضعیت تأهل یک مجرم که به تازگی دستگیر شده است، نظرسنجی کنند. فکر میکنید چند درصد از افراد رأی به مجرد بودن او خواهند داد؟ در یک سناریوی واقعی، خواهید دید که به احتمال زیاد، عدد به دست آمده از باور عمومی مردم، حتی از توزیع خام هم بیشتر است.
درست است که وابستگی آماری میان دو پدیده مجرد/متأهل بودن و مجرم بودن/نبودن وجود دارد؛ اما این که این را به یک رابطه حتمی تقلیل بدهند و دستاویز تبعیض باشد، صحیح نیست. چون در نهایت، در یک زندان، با مفروضات فوق، بیش از نصف مجرمین، متعلق به گروهی خواهند بود که انتظار را نداریم.
البته اینجا همه اعداد فرضی بودند و برای محاسبه درست، باید به دادههای واقعی و میدانی دسترسی داشت. هدف اصلی، این بود که نشان داده شود، واقعیت نهایی، «میتواند» با پیشفرضهای اولیه یکسان نباشد و حتی متناقض باشد. منظور نشان دادن «امکان» وجود اشتباه در این پیشداوریها بود.
این موضوع، برای سایر انواع پیشداوریها هم میتواند مطرح باشد. از جمله رایجترین این موارد، مکانیزم گزینش و استخدام در نهادهای دولتی است. کسی که برخی معیارهای اعتقادی را نداشته باشد، قاعدتا جذب نمیشود؛ اما باید دید که آیا این پیشفرضها با نتایج عملی همخوانی دارند یا نه؟




لیلا
سلام.
موضوع و متن جالبی بود.
مصطفی
سلام. واقعا زاویه دید زیباییه.